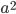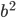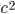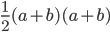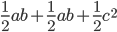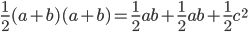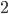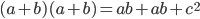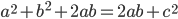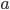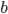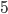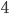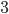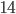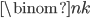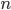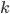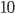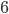Hello everyone!

Welcome back to Pythagoras Week.  If you missed it, be sure to check it out from the beginning.  Today, we're going back to ancient Greece to look at Euclid's proof of the Pythagorean Theorem.  It's not the most elegant proof, but it concludes Euclid's Elements, which is easily the most significant work in the history of math.

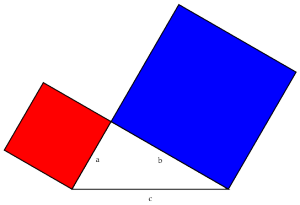
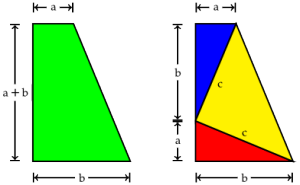
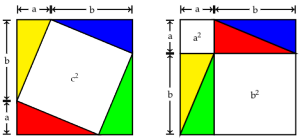
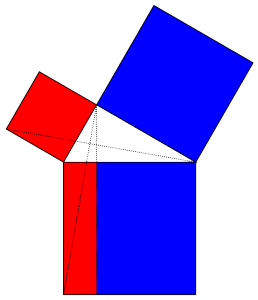
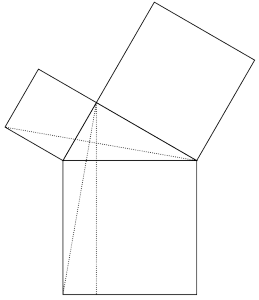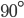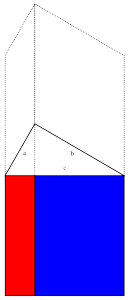
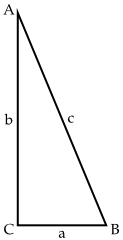
Once again, we begin with our right triangle.  This time, we'll draw a square on each of the three sides.  We'll also draw a few extra lines, as shown below.The first thing to notice is that the two triangles shown in red below are the same (congruent), just rotated by .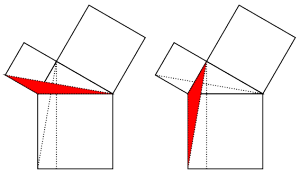The triangle in the left diagram above shares a base and height with the red square in the diagram below, and the triangle in the right diagram above shares a base and height with the red rectangle below.  The two triangles have the same area, so by the area formulas, the red square and rectangle have the same area.  By the same logic, the blue square and rectangle must also have the same area.  As in yesterday's proof, we get .

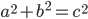There's a lot of interesting history surrounding this, and I'll be sure to go into detail at some point, but that's it for today.  See you again with a new post tomorrow.

by

Hello everyone!

Welcome back to Pythagoras Week.  If you missed it, be sure to check it out from the beginning.  Today's proof uses an interesting "sliding" property of parallelograms.  Essentially, we can take a parallelogram and slide opposite sides parallel to each other without changing the area, as below.  It works because the area for a parallelogram is the base times the height, and we aren't changing either by sliding them.

Now that we have that fact, what can we do with it?  Well, let's start with our right triangle, as below.  We can place squares on either of the legs, as shown.Using the sliding property, we can slide the two squares until they meet, as shown below.Then we can just slide the two parallelograms down until they fill the square at the bottom.The original squares had area and , and the final square has area , so we get .

I've glossed over a lot of steps here because I want to get the big picture across, but if you'd like me to fill in the details, I'm happy to explain in the comments.

That's it for today.  Tune in tomorrow for another proof.

by

Hello everyone!

Welcome back to Pythagoras Week.  If you missed yesterday's post, be sure to check it out.  Today, I'd like to show you a proof originally given by President James Garfield.

Suppose once again we have a right triangle with sides .  Construct a trapezoid with the dimensions shown below on the left.  As you might recall, the area of a trapezoid is half the sum of the bases times the height.  Thus, the area of the trapezoid on the left is .  Next, break this trapezoid into three right triangles, as show at the right.  The area of a triangle is half the base times the height.  Thus, the total area of the three triangles is .We've got the same trapezoid, so the two areas must be the same.  Thus, .  Multiplying both sides by , we get .  With a little algebra, we get .  Thus, .

That's it for today.  Join me again each day this week for another proof.

by

Hello everyone!

One of the most beautiful features of math is that it allows us to solve the same problem in lots of different ways.  So every day this week, I'm going to post a proof of the Pythagorean Theorem.  The proofs I've chosen all come from very different parts of geometry.  I hope you'll appreciate that there's rarely only one way to prove something, and there are many perspectives we can take.

First, let's define some terms.  A right triangle is a triangle with a right angle (or  angle), as below.  The short sides next to the right angle are called legs, and the long side opposite the right angle is the hypotenuse.  For convenience, we'll name the vertices (corners) with capital letters, and we'll name the sides with lowercase letters.Now, the Pythagorean Theorem states that .  That is, the squares of the lengths of the legs add to the square of the hypotenuse.  Or, more geometrically, the combined area of a square of side length and a square of side length is the same as the area of a square with side length .

We'll start with one of the simplest proofs.  Let's take a right triangle with side lengths and make four copies of it.  We'll put them into a square of side length in two different ways, as below.In the first arrangement, the space not covered by triangles is a square with side length .  In the second, it's two squares with side lengths and .  We've covered the same area with triangles in both cases, so the area left over has to be the same.  Therefore, .

That's all for today.  Remember to check back every day this week for a new proof.

by