Hello everyone!

Welcome back to Pythagoras Week.  If you missed yesterday's post, be sure to check it out.  Today, I'd like to show you a proof originally given by President James Garfield.

Suppose once again we have a right triangle with sides 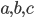.  Construct a trapezoid with the dimensions shown below on the left.  As you might recall, the area of a trapezoid is half the sum of the bases times the height.  Thus, the area of the trapezoid on the left is 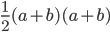.  Next, break this trapezoid into three right triangles, as show at the right.  The area of a triangle is half the base times the height.  Thus, the total area of the three triangles is 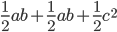.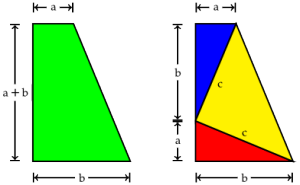We've got the same trapezoid, so the two areas must be the same.  Thus, 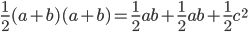.  Multiplying both sides by 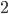, we get 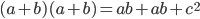.  With a little algebra, we get 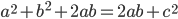.  Thus, .

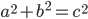That's it for today.  Join me again each day this week for another proof.

by