Hello everyone!

This week, I'd like to talk about permutations.  A permutation of a list is another list with the same elements in some order.  For instance, imagine a deck of playing cards.  Any way you shuffle the cards, you get the same cards, but you might get a different order.  So the resulting ordering is a permutation of the original ordering.

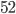It turns out that for permutations, the specific items in our list don't matter all that much.  We can rename the items in the list however we like.  For instance, we could take our deck of cards and give each a different color, or we could number them .  Then we can think of shuffling the cards as rearranging colors or permuting the numbers through .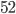

 

The first thing we might want to know is how many permutations of 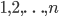there are.  For instance, when , we have 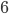permutations, as shown below.

 

To answer more generally, let's look at each element of our list.  There are possible values that our list could start with.  We can't reuse this first value, so there are 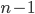values that could come next.  We can't reuse either of these values, so there are 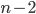possibilities for the next value.  And so on, until we're left with only one choice for the last value.  That gives us 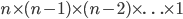total permutations.  That formula's a bit unwieldy, and it shows up a lot, so we usually simplify it to 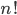(pronounced " factorial").  Thus, there are 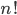permutations of elements.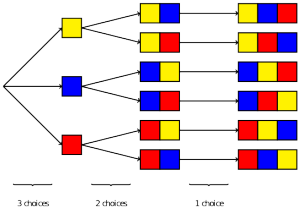

We're talking about combinatorics here, so let's count that a different way.  Say we color the numbers red and the numbers blue.  How many ways can we permute them now?First, let's choose which positions end up with a red number.  We're trying to place numbers, and 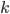of them are red, so we have 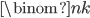ways to pick red numbers.  (If you don't remember this symbol, I talked about it in a previous post.)  We then have to pick an order for the red numbers, which as we saw earlier, can happen in 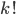ways.  We also have to arrange the blue numbers, which can happen in 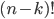ways.  Putting it all together, we get 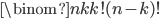permutations.But as we saw earlier, there are also 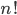permutations.  So 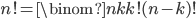.  Rearranging, we get 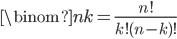.  This gives us a nice formula for our binomial coefficients!

 

There's plenty more to say about permutations.  They lead naturally into topics like cycle decomposition, symmetric groups,  and derangements.  If you'd like to know more, I'm happy to talk about things in the comments.

by