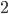Monthly Archives: April 2014

Math, Statistics

Normal Distribution

Leave a comment

Hello everyone!

Sorry for missing last week's update.  Life got in the way.

This week, I'd like to talk about statistics.  A lot of statistics courses focus on how to apply techniques to problems.  If you've studied any statistics, you're probably familiar with things like t-tests, -squared values, and lots of other esoteric tools.  But very few courses go into where those techniques come from or why they work.  Today, we'll look at the normal distribution (or bell curve).

Let's begin with a simple game.  Say we have a fair 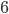-sided die.  Then any number from one to six is equally likely to come up.  We can represent this with a histogram, as below.1d6 Continue reading Normal Distribution →

Facebooktwitterredditpinterestlinkedinmailby feather
Applications, Graph Theory, Math

Fighting Terrorism with Graph Theory

Leave a comment

Hello everyone!

Thus far, I've only talked about the theoretical side of math.  This week, I'd like to change gears and talk about applications.  In particular, let's look at how we might break up terrorist networks using graph theory.

With that out of the way, what's graph theory?  Essentially, graph theory is the study of connections.  A graph is a collection of nodes (also known as vertices or points) connected by edges (also called arcs).  Visually, we can represent a graph by drawing circles to represent the nodes, then connecting them with lines or curves, as below.  It doesn't matter if the lines cross (although there's some interesting theory behind that).  What matters is which nodes are connected.simple_network Continue reading Fighting Terrorism with Graph Theory →

Facebooktwitterredditpinterestlinkedinmailby feather
Math, Set Theory

To Infinity and Beyond

Leave a comment

Hello everyone!

This week, I'd like to talk to you about the infinite.  I'll warn you now, the whole subject is difficult and incredibly counter-intuitive.  Georg Cantor, the guy who first figured most of this stuff out, went crazy, and a lot of his contemporaries found his ideas too radical to believe.  So don't worry if you don't get it right away.  This one's hard.

To get our first taste of infinity, let's begin with Galileo's paradox (yes, that Galileo).  Line up the whole numbers () next to their squares, as shown below.  Now, we've paired each one of the whole numbers with one of the square numbers, so it might be reasonable to say that there are exactly as many whole numbers as square numbers.  But hold on a second - all of the square numbers are already whole numbers, and lots of whole numbers (like ) aren't square, so there should be less squares than whole numbers!  What's going on here?galileo Continue reading To Infinity and Beyond →

Facebooktwitterredditpinterestlinkedinmailby feather