Hello everyone!
Last week, we talked about the Towers of Hanoi. Today, I'd like to look at the same problem from a totally different direction. As before, we begin with three pegs and a bunch of disks. This time, though, we're not so concerned with stacking all the disks on one peg. Instead, let's look at all the possible arrangements of disks.
[IMAGE HERE SOON]
It's a bit cumbersome to work with pictures of pegs and disks (and I'll admit I don't have the patience to draw the diagrams). It would be much easier if we had a way to translate them into something we understand well: lists of numbers.
[IMAGE HERE SOON]
How do these correspond? The number in position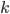 
tells us which peg disk 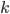is on. The disks on each peg have to be in order of size, so knowing which pegs are on which disks uniquely gives us the arrangement.
Now that we know how arrangements and lists correspond, let's count the arrangements. Say we have 
disks. This gives us a list of length . There are three possibilities for each number (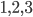
). Thus, there are 
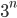possible arrangements.
Now for the really interesting part. We know how many arrangements are possible with disks. Let's draw all these positions as nodes in a graph. We'll draw in edges when there's a legal move connecting two positions. If we've only got one disk, we just get the triangle below, corresponding to moving that disk to any peg.
[IMAGE HERE SOON]
What happens when we add another disk? Or two? We get the graphs below.
[IMAGE HERE SOON]
Notice that the circled parts of the graph for three disks look exactly like the graph for two. This isn't a coincidence; wherever the largest disk is, we can move the smaller disks as if it isn't there. But the largest disk can only move from one peg to another when all the other disks are stacked on the third peg. So the graph for three disks is just three copies of the graph for two, with one edge connecting each copy. Of course, this generalizes, and we can build the graph for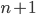 
disks from three copies of the graph for .
The shape of the graph might look familiar too. It's a fractal known as the Sierpinski gasket (closely related to the Sierpinski triangle [LINK HERE]). We'll talk about fractals in depth in another post.
That's it for today. I'll be back again next week to talk about permutations.
by 