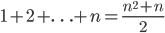Hello everyone!

This week, I'd like to talk about one of my favorite methods of proof: the Pigeonhole Principle.  It can be used to prove some rather profound results, but the basic concept is quite intuitive.  Say we have 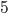pigeons and 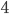holes and, for some reason, we want to place pigeons into holes.  There are a lot of ways to do so, but however we place the pigeons, some hole must end up with at least two pigeons in it.  In general, if we have more pigeons than holes, some hole has to end up with at least two pigeons.  That's the Pigeonhole Principle.

Continue reading Pigeonhole Principle →

by

Hello everyone!

Induction is one of the most useful proof techniques available.  The basic idea is fairly simple: one case works because the previous case worked.  That's sort of abstract, so let's dive into an example.

There's a famous story (in the mathematical world) about an 7-year-old Gauss calculating in a few seconds.  Let's generalize this a bit to show that .  There are a lot of ways to see this, but this week's theme is induction, so let's try that. Continue reading Induction →

by