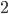Category Archives: Set Theory

Analysis, Math, Set Theory

Real Numbers

Leave a comment

Hello everyone!

I said a few weeks back that I'd define the real numbers for you.  That's what I'd like to do today.  Last time I mentioned the real numbers, I said we could think of them as infinite decimals.  That is a useful way to think of them for a lot of purposes, but it doesn't really give us a way to work with them rigorously.

To start with, let's take a few big steps back.  There are a lot of real numbers (uncountably many, in fact), so let's work with something simpler.  Say for the moment all we have is the number .  We could actually go further back than that, but it's not easy to rigorously define , so for now, that's a good start.

Continue reading Real Numbers →

Facebooktwitterredditpinterestlinkedinmailby feather
Math, Set Theory

To Infinity and Beyond

Leave a comment

Hello everyone!

This week, I'd like to talk to you about the infinite.  I'll warn you now, the whole subject is difficult and incredibly counter-intuitive.  Georg Cantor, the guy who first figured most of this stuff out, went crazy, and a lot of his contemporaries found his ideas too radical to believe.  So don't worry if you don't get it right away.  This one's hard.

To get our first taste of infinity, let's begin with Galileo's paradox (yes, that Galileo).  Line up the whole numbers () next to their squares, as shown below.  Now, we've paired each one of the whole numbers with one of the square numbers, so it might be reasonable to say that there are exactly as many whole numbers as square numbers.  But hold on a second - all of the square numbers are already whole numbers, and lots of whole numbers (like ) aren't square, so there should be less squares than whole numbers!  What's going on here?galileo Continue reading To Infinity and Beyond →

Facebooktwitterredditpinterestlinkedinmailby feather