Hello everyone!

Welcome back to Pythagoras Week.  If you missed it, be sure to check it out from the beginning.  Today's proof uses an interesting "sliding" property of parallelograms.  Essentially, we can take a parallelogram and slide opposite sides parallel to each other without changing the area, as below.  It works because the area for a parallelogram is the base times the height, and we aren't changing either by sliding them.

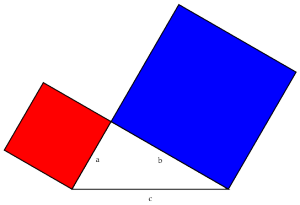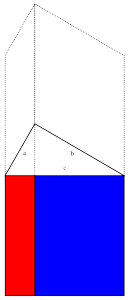Now that we have that fact, what can we do with it?  Well, let's start with our right triangle, as below.  We can place squares on either of the legs, as shown.Using the sliding property, we can slide the two squares until they meet, as shown below.Then we can just slide the two parallelograms down until they fill the square at the bottom.The original squares had area 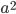and 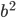, and the final square has area 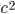, so we get .

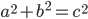I've glossed over a lot of steps here because I want to get the big picture across, but if you'd like me to fill in the details, I'm happy to explain in the comments.

That's it for today.  Tune in tomorrow for another proof.

by