Hello everyone!

This week, I'd like to talk to you about the infinite.  I'll warn you now, the whole subject is difficult and incredibly counter-intuitive.  Georg Cantor, the guy who first figured most of this stuff out, went crazy, and a lot of his contemporaries found his ideas too radical to believe.  So don't worry if you don't get it right away.  This one's hard.

To get our first taste of infinity, let's begin with Galileo's paradox (yes, that Galileo).  Line up the whole numbers () next to their squares, as shown below.  Now, we've paired each one of the whole numbers with one of the square numbers, so it might be reasonable to say that there are exactly as many whole numbers as square numbers.  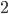But hold on a second - all of the square numbers are already whole numbers, and lots of whole numbers (like ) aren't square, so there should be less squares than whole numbers!  What's going on here?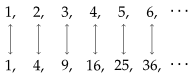

Well, there are two key ideas at play here.  First, we say that two sets are the same size if we can match up their elements (or create a bijection, if you like fancy terms).  So we can say the set of whole numbers, the set of non-negative integers, and the set of integers (as shown below) all have the same size.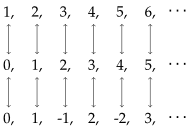The second is that a set is called infinite if it has a subset that's the same size.  So the whole numbers are infinite, because the set is the same size as the squares, but 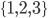is finite, because every subset has at most two elements.

Now, thus far we've only seen infinite sets that are the same size.  One question you might ask is whether it makes sense to say one infinite set is bigger than another.  As it turns out, it does!  Let's look at an example.  We'll see there are more real numbers than whole numbers.

First, let's talk about the real numbers.  When you learned about decimals, you probably heard that the digits can go on forever past the decimal point.  If you look at all combinations of digits, we get a set of numbers called the real numbers.  I'll be more rigorous about this in another post, but for now, this definition is good.

There are a lot of real numbers, so to make things a little simpler, let's just look at the ones between and .  Assume, for the moment, that there are just as many such numbers as there are whole numbers.  Then we list them all out next to the whole numbers, as below.Now let's find one we missed.  Create a new number by taking the first digit (after the decimal point) of the first number, the second digit of the second number, and so on, as shown, and replacing them all with something different.  This number can't be matched with , because it differs in the first digit after the decimal point.  It can't be matched with 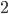, because it differs in the second.  And for any 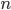, it can't be matched with 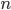, because it differs in the 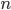th digit.  So we've got a number between and which isn't matched with any whole number.  But we assumed we matched them all, so that can't be right.  Then our assumption that there are as many whole numbers as real numbers between and must be wrong, and there are more real numbers than whole numbers.I'll leave you with one last thought.  We've seen that there are different sizes of infinity, and we've seen that there are more real numbers than whole numbers.  It natural to ask if there's a size of infinity between these two.  This problem, called the Continuum Hypothesis, fundamentally shook the foundations of set theory.  As it turns out, it depends how you construct mathematics.  You can actually build a version of math where such an infinity exists and another version where it doesn't, and both are completely valid.

by