Hello everyone!

I'm back, and I've got lots of exciting math to share, so let's get to it!  This week, I'd like to talk about a classic puzzle called the Towers of Hanoi.  To start, we have a board with three pegs, as shown below, one of which has a stack of disks on it.  We want to move all the disks from the starting peg to either of the other pegs.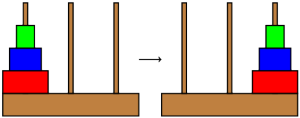However, we have two constraints: we can only move one disk at a time, from one peg to another, and we can never place a disk on top of a smaller disk.  So in the example below, we can move the middle disk onto the larger disk on the left, but not the smaller disk on the right.

So how do we solve it?  The key insight here is that a disk can only move when all the smaller disks are stacked on another peg.  So in the example below, we can only move the red disk to the third peg once we've moved the yellow, green, and blue disks to the second.  So the problem of moving all four disks can be broken down into moving the top three to another peg, moving the largest disk, then moving the top three back on top of the largest. 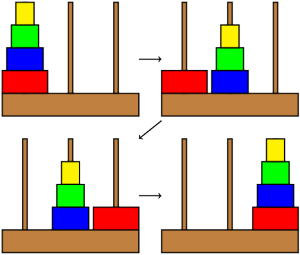This brings up an important concept.  We've taken the problem with 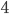disks and reduced it to the problem with 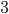.  Or, more generally, we've reduced the problem with 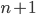disks to the problem with .  We've found a procedure for solving the problem given a procedure for solving the same problem in a smaller case.  We call such a procedure a recursive algorithm.  (If this reminds you of induction, you're absolutely on the right track.)

Next, we might wonder how many steps it takes to solve the Towers of Hanoi.  With disk, we only need step: just move the disk to another peg.  With 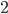disks, we need to move disk to one peg, disk 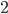to another, then disk back onto disk 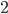, for a total of 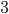moves.  With 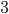disks, we need 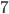moves, and with 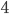disks, we need .  What's the pattern here?

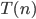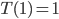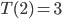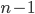Let's call the number of steps it takes to move disks to another peg.  Then , , and so on.  As we saw above, we can move disks by moving twice, with an extra move in the middle.  Thus, 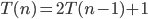.  This relationship lets us solve to get .

There are a lot of ways we might extend the Towers of Hanoi.  The simplest way is to add a fourth peg.  It turns out this makes the problem of finding the shortest sequence of moves hard.  In fact, no one has solved it yet; it remains an open problem.  If you're curious, I'd love to discuss it further in the comments.

There's much more that can be said about the Towers of Hanoi, so I've devoted next week's post to one feature that I find particularly cool.  I hope you'll join me then.

by