Hello everyone!

I was playing around with continued fractions last week, and I stumbled across a nice pattern that I hadn't seen before.  I thought it might be interesting to talk about it here.

 

Let's start with a motivating question.  Consider the number below:

,

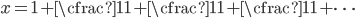extending on infinitely.  It's possible to prove that continued fractions always converge (that is, they come out to actual numbers), so 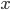is well-defined.  So what's its value?

Given what 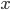looks like, we might try looking at .  When we do, we get

.

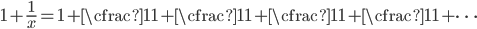But that expression on the right side is just 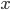.  So we have 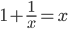.  Rearranging, we get 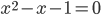.  By the quadratic formula, we get 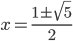.  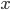is positive, so we get .

This number might look familiar; it's known as the golden ratio, 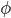.  It shows up everywhere in nature, it's fundamental in music and art, and it has a lot of interesting mathematical properties.  For today, let's show that it's intimately related to the Fibonacci sequence.

Recall that the Fibonacci numbers, 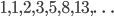, are what we get when we start with 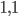and get each term by adding the previous two together.  What happens if we divide consecutive terms?

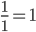
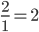
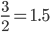
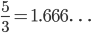
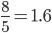
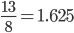
If we keep going, we see ratios seem to be getting close together.  In fact, they seem to be bouncing back and forth across a point somewhere near .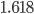

Given that I talked about the golden ratio earlier, you might guess that the ratios are converging to 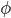.   And in fact, they are.  Why?  Let's look at the continued fraction we started with, but instead of going out to infinity, stop part way.  That is, let's look at the convergents of the continued fraction.

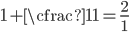
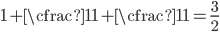
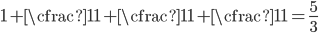
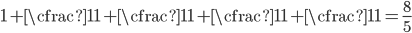
The more ones we add on the left side, the closer we get to 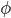.  But the numbers on the right are just the ratios of consecutive Fibonacci numbers.  (Do you see why?)  So they must also get closer to .

 

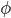There's actually another very nice connection between the Fibonacci numbers and 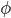.  Binet's formula relates them directly:

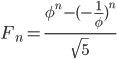
This is a rather magical fact, so I'll prove it in a later post.

That's it for today.  I'll see you next week.

by