Hello everyone!

Sorry for missing last week's post.  I was a bit busy graduating.  It shouldn't happen again.

I mentioned back in my first post that one of my interests is algorithm design.  This week, I'd like to talk a bit about what that means.  The word "algorithm" gets thrown around a lot in TV shows, movies, and science journalism, and quite often, it's horribly misused.  So let's define our terms before we go further: an algorithm is a sequence of steps which can be followed to turn one form of data into another.

That's kind of an abstract definition, though, so let's dive in with an example.  Let's say we have a list of numbers, and we'd like to know which is the largest.  How might we go about this?  One way to do this is to just walk through the list and keep track of the largest number we've seen.  So in the list below, we start by saying the 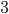is the largest number.  Next, we check the 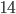and see that it's larger than 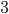, so it's the largest so far.  We then check the and see that it's even larger.  Finally, we see that the isn't larger, so is still the largest we've seen.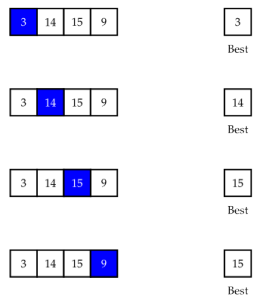

The solution above is good, but there are other ways to solve the problem.  Another approach we might take is to check if each element is the largest.  To do so, we compare each element against every other element, and if nothing is larger, we declare it the largest.  So in the example below, we compare 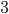with every other element and find that there's something larger (namely 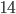).  Then we compare 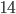against every other element and find that is larger.  Then we compare against everything and see that it is the largest.  We could stop there, but for the sake of completeness, we also check to see that isn't the largest.

 

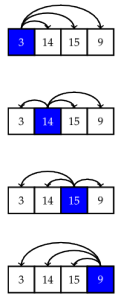
Both of the algorithms described above can find the largest element of a list.  If all that mattered was getting the answer, we might say they were equally good.  But if we want to use these in the real world, we also need to take speed into account, particularly when the list gets very long.  So how do we quantify speed?  One way we could do it to just run the two algorithms on a computer with some test data.  We would get curves like the ones below for the time taken.But this can be very misleading.  How do we know the trends we see with small data sets continue when the data set gets larger.  In other words, how do we know that the graph above isn't just a part of the graph below?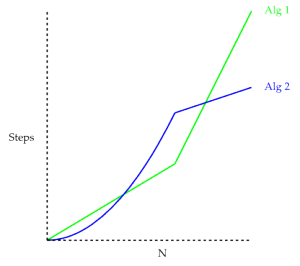

 

We answer this by counting the number of steps taken for each algorithm.  In general, an algorithm that takes more steps needs more time to run, so we want to use as few steps as possible.  Let's say our list has length .  The first algorithm compares each element of the list against the largest we've seen thus far.  That's one comparison for each element, for a total of comparisons.  The second algorithm compares each pair of elements of our list, but doesn't compare each element with itself.  There are 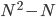such pairs that we can make, so the second algorithm takes at most 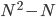steps.

Generally speaking, it's not necessary to get the exact number of steps needed.  What's more important is how the number of steps scales as the problem size increases.  For instance, what happens if we double the length of the list?  For the first algorithm, we need at most steps, and doubling doubles the time needed.  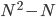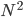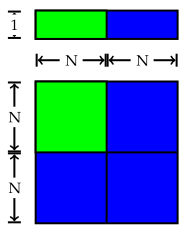However, for the second, we need , which is approximately steps, and doubling quadruples 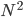, so the time needed quadruples.  We can see this below: doubling doubles the area of the first green rectangle () but quadruples the area of the second ().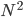

 

It turns out the most useful measure of how an algorithm scales is the largest power of in the number of steps, which we denote with an O (pronounced Big-Oh).  There's a more rigorous definition, but for now, this will do.  The largest power of in is , so we say that the first algorithm is 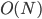.  The largest power in 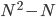is 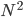, so the second algorithm is 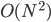.  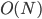The lowest powers of scale better as gets large, so an algorithm is generally faster with large data sets than an 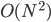algorithm.  Thus, we would call the first algorithm better than the second.  This method, known as asymptotic analysis, is really the cornerstone for the study of algorithms.  I'll explain this in a lot more detail in future posts, so don't worry if you didn't get it here.

by