Hello everyone!

One of the most beautiful features of math is that it allows us to solve the same problem in lots of different ways.  So every day this week, I'm going to post a proof of the Pythagorean Theorem.  The proofs I've chosen all come from very different parts of geometry.  I hope you'll appreciate that there's rarely only one way to prove something, and there are many perspectives we can take.

First, let's define some terms.  A right triangle is a triangle with a right angle (or 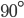 angle), as below.  The short sides next to the right angle are called legs, and the long side opposite the right angle is the hypotenuse.  For convenience, we'll name the vertices (corners) with capital letters, and we'll name the sides with lowercase letters.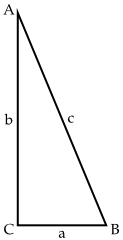Now, the Pythagorean Theorem states that 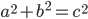.  That is, the squares of the lengths of the legs add to the square of the hypotenuse.  Or, more geometrically, the combined area of a square of side length 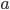and a square of side length 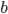is the same as the area of a square with side length .

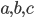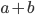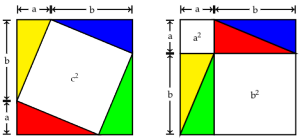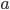We'll start with one of the simplest proofs.  Let's take a right triangle with side lengths and make four copies of it.  We'll put them into a square of side length in two different ways, as below.In the first arrangement, the space not covered by triangles is a square with side length .  In the second, it's two squares with side lengths and 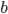.  We've covered the same area with triangles in both cases, so the area left over has to be the same.  Therefore, .

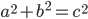That's all for today.  Remember to check back every day this week for a new proof.

by