Hello everyone!
I said a few weeks back that I'd define the real numbers for you. That's what I'd like to do today. Last time I mentioned the real numbers, I said we could think of them as infinite decimals. That is a useful way to think of them for a lot of purposes, but it doesn't really give us a way to work with them rigorously.
To start with, let's take a few big steps back. There are a lot of real numbers (uncountably many, in fact), so let's work with something simpler. Say for the moment all we have is the number 
. We could actually go further back than that, but it's not easy to rigorously define , so for now, that's a good start.
So what can we do here? We only have one value to work with, so we need a way to generate more. The first thing we can do is define addition. That works pretty much as you'd expect. We can define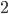 
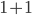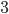as 
, 
as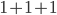 
, and so on. Addition is associative, so addition of these new numbers works right too. For example, 
.
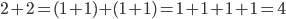Once we have addition, we have a set of numbers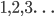 
called the natural numbers, or 
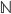. That's a good start, but we've missed a lot. For instance, we don't seem to have 
or any negative numbers. We can take a step in the right direction by introducing subtraction. That lets us get and the negatives of all the natural numbers. So we've got a new set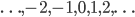 
, called the integers, or 
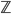. It might make sense to define multiplication next, but it turns out that doesn't give us any new numbers. Instead, we define division for any two integers (excluding division by zero). That gives us the set of fractions, or rational numbers (
).
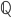However, it turns out that some numbers are not rational.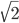 
, for example, cannot be written as a fraction of integers. We also can't get everything by introducing square roots (or cube roots, or roots of arbitrary degree), as it turns out numbers like 
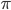(so-called transcendental numbers) can't be made that way. So where do we go from here?
There are two common ways to extend the rational numbers to get the real numbers: Cauchy sequences and Dedekind cuts. They turn out to give us equivalent sets of numbers, but they're different ways of thinking about the reals.
The basic idea behind Cauchy sequences is that we can describe a number by a sequence of progressively smaller intervals containing it. For instance, might be represented by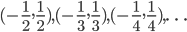 
. Note that the length of the intervals shrinks to . So every future interval has length at most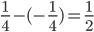 
, and any number more than 
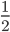away from is outside every interval. In fact, every number other than the one we want to represent is too far away to be in any future interval. Essentially, we squeeze the ends of the interval together until only one value is left. If we use the rational numbers for our endpoints, the values we get are the reals.
The basic idea behind Dedekind cuts is that we can describe a number by what's larger than it. We divide the rational numbers into two sets, where every element of one set is larger than every element of the other. For example, 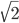might be represented by two sets: those whose squares are less than 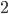(and all the negatives), and those whose squares are more than 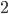. We can similarly define all the real numbers with such a cut.
by 