Hello everyone!

This week, I'd like to talk about one of my favorite methods of proof: the Pigeonhole Principle.  It can be used to prove some rather profound results, but the basic concept is quite intuitive.  Say we have 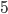pigeons and 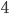holes and, for some reason, we want to place pigeons into holes.  There are a lot of ways to do so, but however we place the pigeons, some hole must end up with at least two pigeons in it.  In general, if we have more pigeons than holes, some hole has to end up with at least two pigeons.  That's the Pigeonhole Principle.

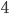In fact, we can take this a step further.  Suppose we have pigeons and holes.  Then however we arrange them, one hole must contain at least 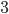pigeons.  Or, in general, if we have 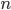holes and at least 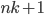pigeons, we have a hole with at least 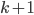pigeons.

Let's try an example.  Say we have a square with side length 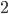, and we're given five points within it, as shown below.  Let's show that two of those points have to be at most 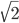away from each other.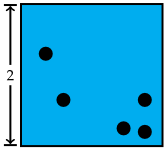We want to use the Pigeonhole Principle here, so the first thing to figure out is what we will use for our holes and our pigeons.  In this case, we'll treat our points as the pigeons.  To get our holes, we can divide the square into quarters, as shown below.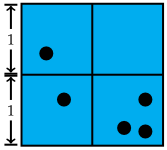Any two points in a square with side are at most as far apart as opposite corners, which (by the Pythagorean Theorem) are a distance of 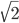apart.  Thus, any two points in the same square are at most 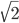apart.  We have 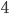squares and 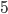points, so by the Pigeonhole Principle we have two points in the same square.  Thus, we have two points that are at most 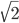apart.

That was a pretty quick example, so let's try another.  Let's say we have 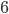different whole numbers from to 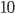.  Let's show that two of them differ by exactly .

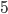We're choosing a bunch of numbers, so it's fair to guess that those will be our pigeons.  Then what should be our holes?  We can pair up the numbers from to 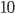, as shown below.  There are 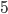pairs, so by the Pigeonhole Principle, two of our numbers must end up in the same pair.  The two numbers in each pair are 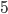apart, so we have a pair of numbers that differ by exactly .

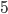by