Hello everyone!
Today, I'd like to talk about one of the most fundamental concepts in combinatorics: binomial coefficients. We define 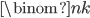 (read "
(read " choose
choose 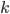 ") to be the number of ways to choose
") to be the number of ways to choose 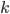 of
of  things. So, for example, there are
things. So, for example, there are 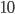 ways to choose
ways to choose 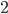 of
of 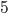 blocks to color red, as shown below.
blocks to color red, as shown below.
Now, this is combinatorics, so most of what we're going to do today is about counting the same thing in two ways. We'll start with the simplest first. Let's show 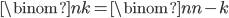 . That is, there are exactly as many ways to choose
. That is, there are exactly as many ways to choose 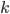 of
of  items as there are to choose
items as there are to choose  of them. Why? Well, there are
of them. Why? Well, there are 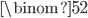 ways we could color
ways we could color 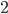 of
of 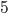 blocks red, as we saw above. But we could just as well choose the other
blocks red, as we saw above. But we could just as well choose the other 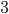 blocks to color blue, as below. So
blocks to color blue, as below. So 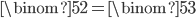 . By the same logic, we get that
. By the same logic, we get that 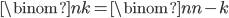 .
.
Let's look at another interesting result: 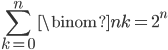 . Why is it true? Let's count all the ways to pick any number of blocks from a row of length
. Why is it true? Let's count all the ways to pick any number of blocks from a row of length  to color red. One way we could see this is to break up the possibilities by the number of red blocks. If we want
to color red. One way we could see this is to break up the possibilities by the number of red blocks. If we want 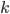 red blocks from our
red blocks from our  total blocks, there are
total blocks, there are 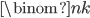 to choose them. Summing over all valid
to choose them. Summing over all valid 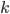 , we get
, we get 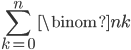 total possibilities.
total possibilities.
Another way to think of it is that for each block, there are two possibilities: red or white. The colors for each are independent, so we can multiply the possibilities together. There are  blocks, each with
blocks, each with 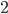 possible colorings, for a total of
possible colorings, for a total of 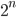 possibilities. We've counted the same colorings with these two methods, so the counts must be equal. Thus,
possibilities. We've counted the same colorings with these two methods, so the counts must be equal. Thus, 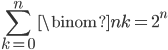 .
.
It turns out binomial coefficients are also related to each other by the recurrence 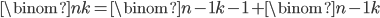 . We already know that
. We already know that 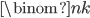 counts the ways to choose
counts the ways to choose 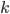 of
of  tiles to color red. So let's find a way to count the same thing to get the other side of the equation. In this case, we can divide the possibilities into those where the last tile is red and those where it isn't. If the last tile is red, then we have
tiles to color red. So let's find a way to count the same thing to get the other side of the equation. In this case, we can divide the possibilities into those where the last tile is red and those where it isn't. If the last tile is red, then we have 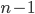 more tiles to choose from, and we want
more tiles to choose from, and we want 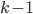 to be red. If it isn't, we want to choose
to be red. If it isn't, we want to choose 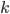 of the remaining
of the remaining 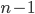 tiles. This gives us
tiles. This gives us 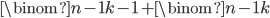 , as we wanted.
, as we wanted. This last relationship gives us a nice way to construct the binomial coefficients. We can place them in a triangle structure, as below. You can see
This last relationship gives us a nice way to construct the binomial coefficients. We can place them in a triangle structure, as below. You can see 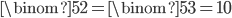 down in the sixth row. From the recurrence above, we know that each number in this triangle is the sum of the two above it. You might have seen this pattern of numbers before. It's known as Pascal's triangle. There are a lot of pretty combinatorial and number theoretic results that come out of it. For today, I'll just mention that this is one way to derive it.
down in the sixth row. From the recurrence above, we know that each number in this triangle is the sum of the two above it. You might have seen this pattern of numbers before. It's known as Pascal's triangle. There are a lot of pretty combinatorial and number theoretic results that come out of it. For today, I'll just mention that this is one way to derive it.
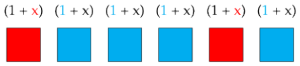
One last thing before I sign off for the day. I've been calling the 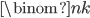 binomial coefficients. Why do they get that name? It turns out that
binomial coefficients. Why do they get that name? It turns out that 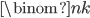 is the coefficient of
is the coefficient of 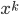 in
in 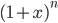 . To see why it works, imagine writing out the
. To see why it works, imagine writing out the  copies of
copies of 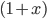 we want to multiply, as below. To get a copy of
we want to multiply, as below. To get a copy of 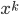 , we must choose
, we must choose 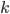 of the
of the  terms to give us an
terms to give us an 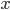 . Equivalently, we can imagine a block for each term which is colored red if we choose the
. Equivalently, we can imagine a block for each term which is colored red if we choose the 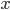 and blue if we choose the
and blue if we choose the  . This can happen in
. This can happen in 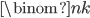 ways, so we get a total of
ways, so we get a total of 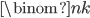 copies of
copies of 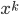 , which we then add together. Thus, the coefficient of
, which we then add together. Thus, the coefficient of 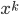 is
is 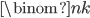 .
.