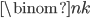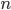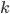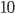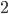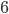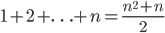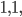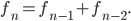Category Archives: Math

Math, Proof Techniques

Pigeonhole Principle

Leave a comment

Hello everyone!

This week, I'd like to talk about one of my favorite methods of proof: the Pigeonhole Principle.  It can be used to prove some rather profound results, but the basic concept is quite intuitive.  Say we have 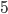pigeons and 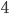holes and, for some reason, we want to place pigeons into holes.  There are a lot of ways to do so, but however we place the pigeons, some hole must end up with at least two pigeons in it.  In general, if we have more pigeons than holes, some hole has to end up with at least two pigeons.  That's the Pigeonhole Principle.php

Continue reading Pigeonhole Principle →

Facebooktwitterredditpinterestlinkedinmailby feather
Analysis, Math, Set Theory

Real Numbers

Leave a comment

Hello everyone!

I said a few weeks back that I'd define the real numbers for you.  That's what I'd like to do today.  Last time I mentioned the real numbers, I said we could think of them as infinite decimals.  That is a useful way to think of them for a lot of purposes, but it doesn't really give us a way to work with them rigorously.

To start with, let's take a few big steps back.  There are a lot of real numbers (uncountably many, in fact), so let's work with something simpler.  Say for the moment all we have is the number .  We could actually go further back than that, but it's not easy to rigorously define , so for now, that's a good start.

Continue reading Real Numbers →

Facebooktwitterredditpinterestlinkedinmailby feather
Math, Statistics

Normal Distribution

Leave a comment

Hello everyone!

Sorry for missing last week's update.  Life got in the way.

This week, I'd like to talk about statistics.  A lot of statistics courses focus on how to apply techniques to problems.  If you've studied any statistics, you're probably familiar with things like t-tests, -squared values, and lots of other esoteric tools.  But very few courses go into where those techniques come from or why they work.  Today, we'll look at the normal distribution (or bell curve).

Let's begin with a simple game.  Say we have a fair -sided die.  Then any number from one to six is equally likely to come up.  We can represent this with a histogram, as below.1d6 Continue reading Normal Distribution →

Facebooktwitterredditpinterestlinkedinmailby feather
Applications, Graph Theory, Math

Fighting Terrorism with Graph Theory

Leave a comment

Hello everyone!

Thus far, I've only talked about the theoretical side of math.  This week, I'd like to change gears and talk about applications.  In particular, let's look at how we might break up terrorist networks using graph theory.

With that out of the way, what's graph theory?  Essentially, graph theory is the study of connections.  A graph is a collection of nodes (also known as vertices or points) connected by edges (also called arcs).  Visually, we can represent a graph by drawing circles to represent the nodes, then connecting them with lines or curves, as below.  It doesn't matter if the lines cross (although there's some interesting theory behind that).  What matters is which nodes are connected.simple_network Continue reading Fighting Terrorism with Graph Theory →

Facebooktwitterredditpinterestlinkedinmailby feather
Math, Set Theory

To Infinity and Beyond

Leave a comment

Hello everyone!

This week, I'd like to talk to you about the infinite.  I'll warn you now, the whole subject is difficult and incredibly counter-intuitive.  Georg Cantor, the guy who first figured most of this stuff out, went crazy, and a lot of his contemporaries found his ideas too radical to believe.  So don't worry if you don't get it right away.  This one's hard.

To get our first taste of infinity, let's begin with Galileo's paradox (yes, that Galileo).  Line up the whole numbers () next to their squares, as shown below.  Now, we've paired each one of the whole numbers with one of the square numbers, so it might be reasonable to say that there are exactly as many whole numbers as square numbers.  But hold on a second - all of the square numbers are already whole numbers, and lots of whole numbers (like ) aren't square, so there should be less squares than whole numbers!  What's going on here?galileo Continue reading To Infinity and Beyond →

Facebooktwitterredditpinterestlinkedinmailby feather
Math, Proof Techniques

Induction

Leave a comment

Hello everyone!

Induction is one of the most useful proof techniques available.  The basic idea is fairly simple: one case works because the previous case worked.  That's sort of abstract, so let's dive into an example.

There's a famous story (in the mathematical world) about an 7-year-old Gauss calculating in a few seconds.  Let's generalize this a bit to show that .  There are a lot of ways to see this, but this week's theme is induction, so let's try that. Continue reading Induction →

Facebooktwitterredditpinterestlinkedinmailby feather
Combinatorics, Math

Fibonacci Tilings

Leave a comment

Hello, everyone!

As I mentioned in my opening post, one of my interests is combinatorics.  Basically, it amounts to counting things cleverly.  It's probably not the most practical field (although it has its uses in statistics and quantum physics), but I find that it has some of the most beautiful and intuitive results.

One of the most studied topics in combinatorics is the Fibonacci sequence.  We start with then we get each other term by adding the previous two.  So the first few terms are .  More algebraically, we have and   Those are nice numbers, I guess, but what do they mean? Continue reading Fibonacci Tilings →

Facebooktwitterredditpinterestlinkedinmailby feather
Geometry, Math

Happy Pi Day!

Leave a comment

Hello, everyone, and Happy Pi Day!

You've almost assuredly seen the number before.  It shows up in all sorts of odd places.  So what is ?  You probably know but that might feel like I'm pulling a number out of the air.  Where does it really come from?

First, let's start with the definition: is the ratio of a circle's circumference to its diameter.  That is, if you took the circle and unrolled it (as below), the line segment you end up with is times the width of the circle at its widest point.

unrollCircle Continue reading Happy Pi Day! →

Facebooktwitterredditpinterestlinkedinmailby feather