Hello, everyone!

As I mentioned in my opening post, one of my interests is combinatorics.  Basically, it amounts to counting things cleverly.  It's probably not the most practical field (although it has its uses in statistics and quantum physics), but I find that it has some of the most beautiful and intuitive results.

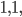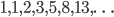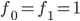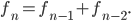One of the most studied topics in combinatorics is the Fibonacci sequence.  We start with then we get each other term by adding the previous two.  So the first few terms are .  More algebraically, we have and   Those are nice numbers, I guess, but what do they mean?

I'll answer that by asking a completely different question.  Let's say we have a bunch of tiles of length 1 (call them squares) and tiles of length 2 (call them dominoes), and we want to tile a row of length 1 with them.  How many ways can we do it?  We can't use any dominoes, so we can only do it using a square.  So there's one way.  What if we want to tile a row of length 2?  We can do it with two squares, or we can use a domino, for a total of two ways.  I've shown the ways to tile rows of length 3, 4, and 5 below.

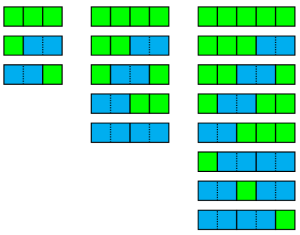Because I started this post by talking about the Fibonacci numbers, you might guess that the number of ways to tile a row of length is 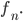  And you'd be absolutely right.  That's an interesting fact, but why is it true?  Let's split the 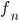tilings of length 5 up by whether they end with a square or a domino, as shown below.

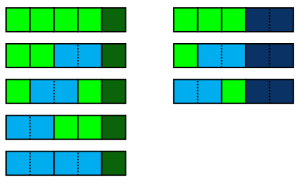If we take the square off the end of any tiling in the first set, we get a tiling of length 4, and if we take the domino off the end of any tiling in the second set, we get a tiling of length 3.  So the number of tilings of length 5 is  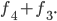 But as we said above, the number of tilings of length 5 is .  These are both valid ways to count the tilings, so they must give us the same number.  Thus, 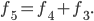  The same logic gives us the formula 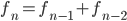we saw earlier.  Since we know the first few cases match the Fibonacci sequence, and we can count the tilings based on the smaller cases by the same formula, we get that the Fibonacci numbers actually count the number of tilings.  That's a pretty spiffy result.

Before I go on to my next example, I want to back up a step.  I mentioned a moment ago that we had two valid ways to count something, so the counts had to be equal.  That seems pretty intuitive, but it's one of the key insights in combinatorics.  Most of the really nice results come from cleverly counting the same thing in two ways.

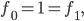
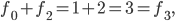
Let's look at another pattern.  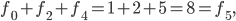and so on.  It seems like the sum of the first few even terms in the Fibonacci sequence gives us the next odd term.  To see why that works, let's try counting something in two ways.  As we saw above, counts the number of ways to tile a row of length 5.  How else might we count the tilings?  In this case, it's useful to partition the possibilities by the position of the last square, as below.  If we do that, we get tilings of lengths 0, 2, and 4, followed by a square and enough dominoes to take the length to 5.  We can do the same thing with any odd length because there always has to be at least one square.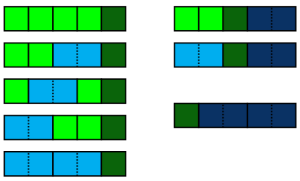

I've really just scratched the surface of what you can do with tilings, and that's just one small piece of what we study in combinatorics.  I hope you'll stay with me to see some more fun results.

by