Hello, everyone, and Happy Pi Day!

You've almost assuredly seen the number 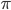before.  It shows up in all sorts of odd places.  So what is 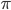?  You probably know but that might feel like I'm pulling a number out of the air.  Where does it really come from?

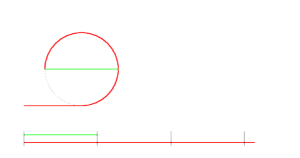
First, let's start with the definition: 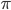is the ratio of a circle's circumference to its diameter.  That is, if you took the circle and unrolled it (as below), the line segment you end up with is 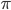times the width of the circle at its widest point.

You've also probably heard that the area of a circle is 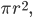where 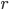is the circle's radius.  That's the same 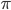that we defined above.  That's an odd coincidence; why might that be true?  Well, lines and rectangles are a lot easier to work with than curvy things like circles (I'll come back to this when I rant about calculus), so let's make our circle look more like a rectangle.  Slice the circle up into wedges, as below, and rearrange them as shown.

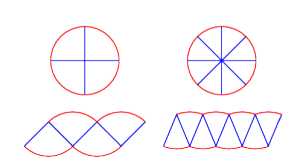The resulting shape isn't quite a rectangle, as the top and bottom are bumpy and the sides are a bit slanted, but the more wedges we cut the circle into, the closer it becomes.  In the limit, that is, as we pretend we can get infinitely many wedges, we actually get a rectangle.  How big is it?  The top and bottom are formed from the circumference of the circle, so the length of each is half the circumference.  The sides each come from the radius of the circle.  So the rectangle is by , and its total area is

Now, I haven't exactly been rigorous here, but I hope I've at least given you some sense of why the circumference and area are so nicely related.

You might also wonder how we get the value   There are a lot of good ways to compute it.  The ancient Greeks and Chinese found 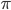by considering inscribed polygons.  Later mathematicians showed 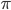was equal to many infinite series.  One of my favorite methods is known as Buffon's Needle.

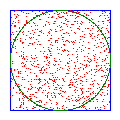
But for today, I'd like to show you a method based on throwing darts.  Imagine you have a square dartboard with side length 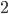, and in it you draw a circle, as shown below.  If you throw a dart at the board (without aiming), how likely is it to land in the circle?

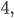The square has area and the circle has area 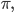so you should hit it roughly 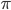times in every 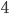throws.  I don't have the patience to throw that many  darts, so I had my computer pick 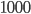random points on the dartboard.  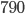of them hit the circle, as shown below, giving me an estimate of  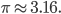 Trying again with 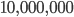points (not shown), I got an estimate of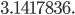

There's a whole lot more that could be said about 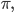but I feel like I'm getting a bit long-winded, so I'll wrap it up here for today.  Have a great Pi Day!

by