Hello everyone!
Induction is one of the most useful proof techniques available. The basic idea is fairly simple: one case works because the previous case worked. That's sort of abstract, so let's dive into an example.
There's a famous story (in the mathematical world) about an 7-year-old Gauss calculating  in a few seconds. Let's generalize this a bit to show that
in a few seconds. Let's generalize this a bit to show that 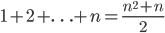 . There are a lot of ways to see this, but this week's theme is induction, so let's try that.
. There are a lot of ways to see this, but this week's theme is induction, so let's try that.
First, we need a base case, that is, a case that we can easily verify. The simplest case is 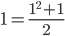 .
.
Now let's assume that 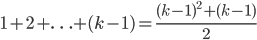 for some
for some 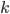 . We showed in our base case that this works for
. We showed in our base case that this works for  , so there's at least once case where this is a valid assumption. This is known as the inductive hypothesis.
, so there's at least once case where this is a valid assumption. This is known as the inductive hypothesis.
Let's show that 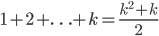 . Rewriting the left side, we get
. Rewriting the left side, we get
 .
.
By our inductive hypothesis, we can substitute to get
 .
.
A bit of algebra gives us 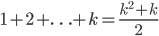 , which is what we wanted to show.
, which is what we wanted to show.
So how do we know this works for all 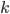 ? We proved already that it works when
? We proved already that it works when 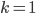 . Why does it work when
. Why does it work when 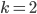 ? We know it works for
? We know it works for 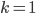 , and as we just saw, that implies it works for
, and as we just saw, that implies it works for 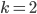 . Why does it work for
. Why does it work for 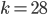 ? We can show it works for
? We can show it works for 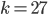 , which follows from when
, which follows from when 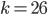 , and so on. So we started with a case that we could show easily, then extended it to work in all cases.
, and so on. So we started with a case that we could show easily, then extended it to work in all cases.
Now that I've bored you with algebra, let's look at a more interesting example. Let's say we have a 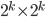 square, with a
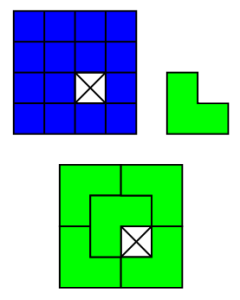
square, with a  square removed, as shown below. We'll see that it can be tiled with so-called L-triominoes, as shown below.
square removed, as shown below. We'll see that it can be tiled with so-called L-triominoes, as shown below.
 First, we need a base case. I'm lazy, so let's take the
First, we need a base case. I'm lazy, so let's take the  case. That is, we want to tile a
case. That is, we want to tile a 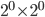 (
( ) square with one square removed. That doesn't actually leave any space left to tile, so we're already done. That was easy! Now we know that it's true when
) square with one square removed. That doesn't actually leave any space left to tile, so we're already done. That was easy! Now we know that it's true when  .
.
As our inductive hypothesis, assume that a 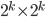 square with one square removed can be tiled. Now let's look at a
square with one square removed can be tiled. Now let's look at a 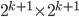 square. The sides have even length, so we can break it into four quadrants, as below. Each of the quadrants is
square. The sides have even length, so we can break it into four quadrants, as below. Each of the quadrants is 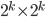 . One of them is missing a square, so by the inductive hypothesis, it can be tiled. It would be nice if the other three were also missing squares, because then we could tile them too. Well, we can't remove squares, but we can cover them with an L-triomino. Place one at the intersection, as shown. Then in every quadrant, there is one square that doesn't have to be covered. By our inductive hypothesis, each quadrant can now be tiled.
. One of them is missing a square, so by the inductive hypothesis, it can be tiled. It would be nice if the other three were also missing squares, because then we could tile them too. Well, we can't remove squares, but we can cover them with an L-triomino. Place one at the intersection, as shown. Then in every quadrant, there is one square that doesn't have to be covered. By our inductive hypothesis, each quadrant can now be tiled.
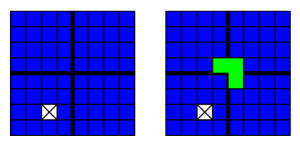 This is one of my favorite examples of induction, but there are plenty of others. If you'd like to test it out for yourself, try using induction to show that
This is one of my favorite examples of induction, but there are plenty of others. If you'd like to test it out for yourself, try using induction to show that  . It works with algebra, but there's a nice geometric way to see it too.
. It works with algebra, but there's a nice geometric way to see it too.