Hello everyone!

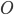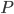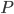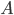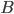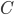Welcome back to Pythagoras Week.  If you missed it, be sure to check it out from the beginning.  Today, we'll use a result known as "power of a point".  Take a circle with center and a point .  Draw a line through that is tangent to the circle at point and another which meets the circle at two points, and , as shown below.  Under these conditions, 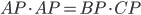.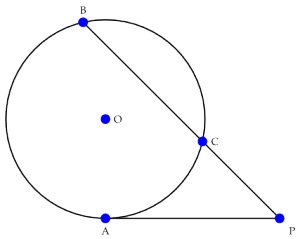The full statement of power of a point is a bit more general, but this will work for today.  We'll use this fact without proof, but if you're curious, a full proof can be found here.

Now let's use power of a point to prove the Pythagorean Theorem.  We'll start with our right triangle 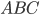.  Draw a circle around 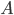which passes through 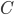.  Extend 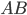to , as shown.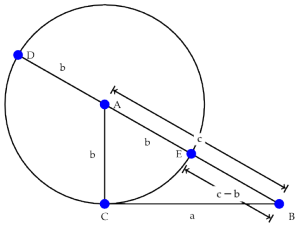Then power of a point gives us 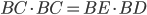.  Writing all these lengths in terms of , we get 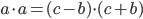.  A little algebra gives us .

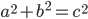That's it for today.  Tune in tomorrow for another proof.

by