Hello everyone!
Welcome back to Pythagoras Week. If you missed it, be sure to check it out from the beginning. Our proof today makes use of similar triangles. We call two triangles "similar" if they have all the same angles, as in the left diagram below. Actually, because the angles in a triangle add to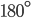 
, we only need to know that two angles are the same to show similarity, as on the right.
The really nice feature of similar triangles is that corresponding sides are all in the same proportions. So if triangles 
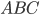and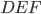 
are similar, then 
.
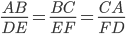Once more, let's take a right triangle 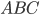with sides 
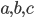, as below. Let's also add a perpendicular line from 
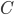to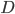 
, as shown, breaking the side into pieces of length 
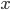and 
.
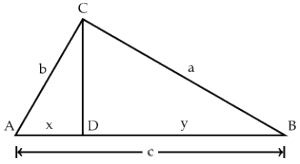Now we've got two smaller triangles, 
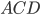and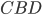 
. Each has a right angle and shares an angle with 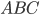, so they both have two angles in common with our original triangle. As we said above, this means they're similar to each other and to .
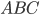As I mentioned earlier, corresponding sides are proportional. So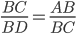 
. Rewriting this in terms of side lengths, we get 
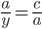, and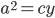 
. Similarly (no pun intended), we get 
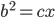. Thus, 
.
Join me tomorrow for one more proof. I promise I've chosen a nice one for last.
by 