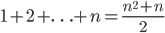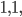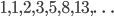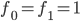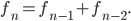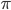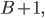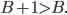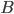Hello, everyone!
Before I launch into the content, I should probably introduce myself. I'm Kyle. I'm currently a college senior studying math and computer science. In particular, I like areas such as combinatorics (fancy counting), graph theory (the study of networks), and algorithms (getting useful information out of lots of data), but my mathematical interests are pretty broad. I'm also a huge fan of puzzles, in pretty much every form. Jigsaws, crosswords, sudoku, chess, etc. I like things that make me stop and think.
So why am I making this blog? I've heard a lot of people say they hate math. The thing is, what they think of as "math" is calculation. It's taking a few numbers, following a set of rules, and arriving at another number. I suppose that could be considered useful, but it's computation, not math. We've invented computers to do that for us. Math is something else entirely. It's useful, it's logical, and, if you ask me, it's beautiful. It's a way of systematically reasoning about the world. It's about proving that assumptions lead to conclusions without any room for doubt.
That's a pretty vague statement, so let me clarify with an example.
You may have heard that the whole numbers (1, 2, 
) go on forever. But how do we know that? Well, let's say they don't. Then there has to be a largest whole number. It has to be pretty big, as it's larger than every other number you can think of, so let's call it 
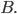What happens if we add one to it? We really don't know much about 
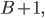but we do know that adding one to any number makes it bigger, so 
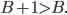But that can't be right; we've got a whole number bigger than 
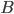when we assumed that 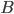was the largest. That means one of our assumptions must have been wrong. The only assumption we made along the way was that there is a biggest whole number, so that must not be true. Thus, the whole numbers must go on forever.
This is a pretty simple example, but we can derive much more interesting results in a lot of fun ways. I hope you'll follow along to see some of the power and beauty of mathematics.
by 
) next to their squares, as shown below. Now, we've paired each one of the whole numbers with one of the square numbers, so it might be reasonable to say that there are exactly as many whole numbers as square numbers. But hold on a second - all of the square numbers are already whole numbers, and lots of whole numbers (like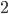 
) aren't square, so there should be less squares than whole numbers! What's going on here?
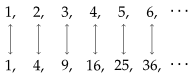Continue reading To Infinity and Beyond 
